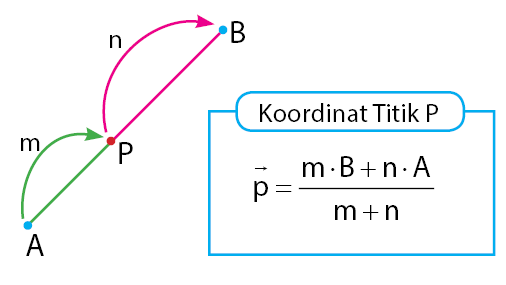
Memahami Perbandingan Koordinat Vektor

Perbandingan koordinat dua vektor adalah konsep fundamental dalam aljabar vektor yang sering dijumpai pada jenjang pendidikan menengah, khususnya di kelas X. Memahami perbandingan ini memungkinkan kita untuk menganalisis hubungan spasial antara dua vektor, seperti apakah vektor tersebut searah, berlawanan arah, atau bahkan saling tegak lurus. Artikel ini akan membahas secara mendalam konsep perbandingan koordinat dua vektor, dilengkapi dengan contoh soal yang relevan dan penjelasannya, sehingga pembaca dapat menguasai materi ini dengan baik.

Outline Artikel:

1. 

   Pendahuluan

   • Pengertian Vektor
   • Koordinat Vektor
   • Pentingnya Perbandingan Vektor

2. Konsep Dasar Perbandingan Koordinat Dua Vektor

   • Vektor Sejajar (Searah dan Berlawanan Arah)
   • Vektor Tidak Sejajar

3. Rumus dan Metode Perbandingan Koordinat

   • Menggunakan Skalar Perkalian
   • Menggunakan Perbandingan Komponen

4. Contoh Soal dan Pembahasan

   • Soal 1: Menentukan Apakah Dua Vektor Sejajar
   • Soal 2: Mencari Nilai Variabel Agar Vektor Sejajar
   • Soal 3: Menentukan Vektor yang Searah/Berlawanan
   • Soal 4: Perbandingan Vektor dalam Konteks Geometri (Segitiga/Jajar Genjang)
   • Soal 5: Vektor di Ruang Tiga Dimensi

5. Aplikasi Perbandingan Vektor dalam Kehidupan Nyata

   • Fisika (Gaya, Kecepatan, Percepatan)
   • Grafika Komputer
   • Navigasi

6. Kesimpulan

1. Pendahuluan

Dalam dunia matematika, vektor adalah objek yang memiliki besaran (magnitudo) dan arah. Konsep vektor sangat penting karena merepresentasikan banyak fenomena fisik dan matematis. Di kelas X, siswa mulai diperkenalkan dengan vektor, terutama vektor dalam dua dan tiga dimensi, yang direpresentasikan menggunakan koordinat.

• Pengertian Vektor: Vektor dapat dibayangkan sebagai sebuah panah yang menunjukkan perpindahan dari satu titik ke titik lain. Arah panah menunjukkan arah vektor, sedangkan panjang panah menunjukkan besaran vektor.

• Koordinat Vektor: Dalam sistem koordinat Kartesius, sebuah vektor dapat direpresentasikan oleh koordinat titik ujungnya, jika titik pangkalnya berada di titik asal (0,0) atau (0,0,0). Misalnya, vektor u yang berpindah dari titik P(x1, y1) ke titik Q(x2, y2) dapat ditulis sebagai u = <x2 – x1, y2 – y1>. Jika pangkal vektor di titik asal, maka vektor u = <x, y> merepresentasikan perpindahan sejauh x satuan pada sumbu-x dan y satuan pada sumbu-y.

• Pentingnya Perbandingan Vektor: Membandingkan dua vektor memungkinkan kita untuk memahami hubungan geometris di antara keduanya. Apakah mereka bergerak ke arah yang sama, berlawanan, atau tidak memiliki arah yang sama sama sekali? Pemahaman ini menjadi dasar untuk konsep-konsep yang lebih kompleks seperti penjumlahan vektor, pengurangan vektor, perkalian skalar, dan perkalian titik (dot product).

2. Konsep Dasar Perbandingan Koordinat Dua Vektor

Dua vektor dikatakan memiliki hubungan perbandingan koordinat jika salah satu vektor dapat diperoleh dari vektor lainnya dengan cara dikalikan dengan sebuah skalar (bilangan real).

• Vektor Sejajar:
  Dua vektor dikatakan sejajar jika arahnya sama atau berlawanan. Secara matematis, vektor a sejajar dengan vektor b jika terdapat sebuah skalar k sedemikian rupa sehingga a = *k*b.

  • Jika k > 0, maka a searah dengan b.
  • Jika k < 0, maka a berlawanan arah dengan b.
  • Jika k = 0, maka a adalah vektor nol, yang memiliki arah tak tentu tetapi dianggap sejajar dengan semua vektor.

  Dalam bentuk koordinat, jika a = <a₁, a₂> dan b = <b₁, b₂>, maka a sejajar dengan b jika perbandingan komponen-komponennya sama:
  a₁/b₁ = a₂/b₂ (dengan syarat b₁ ≠ 0 dan b₂ ≠ 0).
  Atau, bisa juga ditulis sebagai a₁ = k b₁ dan a₂ = k b₂ untuk suatu skalar k.

• Vektor Tidak Sejajar:
  Jika dua vektor tidak dapat dinyatakan sebagai kelipatan skalar satu sama lain, maka kedua vektor tersebut tidak sejajar. Ini berarti tidak ada skalar tunggal yang dapat mengubah satu vektor menjadi vektor lainnya. Dalam konteks koordinat, perbandingan komponen-komponennya tidak akan sama.

3. Rumus dan Metode Perbandingan Koordinat

Ada dua cara utama untuk memeriksa perbandingan koordinat antara dua vektor:

• Menggunakan Skalar Perkalian:
  Jika kita memiliki dua vektor u = <u₁, u₂> dan v = <v₁, v₂>, kita dapat memeriksa apakah ada skalar k sedemikian rupa sehingga u = *kv.
  Ini berarti:
  u₁ = k v₁
  u₂ = k * v₂

  Untuk menemukan k, kita bisa membagi komponen yang bersesuaian (asalkan penyebutnya tidak nol):
  k = u₁ / v₁
  k = u₂ / v₂

  Jika nilai k yang diperoleh dari kedua perbandingan tersebut sama, maka vektor u dan v sejajar.

• Menggunakan Perbandingan Komponen:
  Metode ini merupakan penyederhanaan dari metode skalar perkalian. Jika u = <u₁, u₂> dan v = <v₁, v₂>, maka u sejajar dengan v jika:
  u₁ / v₁ = u₂ / v₂

  Atau, jika kita ingin menghindari pembagian (terutama jika ada komponen yang bernilai nol), kita bisa menggunakan perkalian silang:
  u₁ v₂ = u₂ v₁

  Kedua bentuk perbandingan ini ekuivalen. Jika persamaan ini terpenuhi, maka vektor u dan v sejajar.

  Untuk vektor di ruang tiga dimensi, a = <a₁, a₂, a₃> dan b = <b₁, b₂, b₃>, syarat sejajar menjadi:
  a₁/b₁ = a₂/b₂ = a₃/b₃
  Atau, dalam bentuk perkalian silang untuk memastikan konsistensi:
  a₁ b₂ = a₂ b₁
  a₂ b₃ = a₃ b₂
  a₁ b₃ = a₃ b₁
  (Perhatikan bahwa ketiga kondisi ini perlu dipenuhi jika semua komponen tidak nol, atau kita bisa menggunakan pendekatan yang lebih umum dengan mencari skalar k).

4. Contoh Soal dan Pembahasan

Mari kita terapkan konsep-konsep di atas melalui beberapa contoh soal.

Soal 1: Menentukan Apakah Dua Vektor Sejajar

Diketahui vektor p = <4, -6> dan vektor q = <-2, 3>. Tentukan apakah vektor p dan q sejajar.

Pembahasan:
Kita akan menggunakan metode perbandingan komponen.
Komponen x dari p adalah 4, komponen y adalah -6.
Komponen x dari q adalah -2, komponen y adalah 3.

Perbandingan komponen x:
p₁ / q₁ = 4 / -2 = -2

Perbandingan komponen y:
p₂ / q₂ = -6 / 3 = -2

Karena kedua perbandingan menghasilkan nilai yang sama (-2), maka vektor p dan q sejajar.
Kita juga bisa melihatnya sebagai perkalian skalar:
p = <4, -6>
q = <-2, 3>
Apakah ada skalar k sehingga p = *kq?
4 = k (-2) => k = 4 / -2 = -2
-6 = k (3) => k = -6 / 3 = -2
Karena nilai k* konsisten (-2), maka p = -2q. Ini berarti vektor p sejajar dengan q dan berlawanan arah.

Soal 2: Mencari Nilai Variabel Agar Vektor Sejajar

Diketahui vektor a = <x, 6> dan vektor b = <3, -9>. Agar vektor a sejajar dengan vektor b, tentukan nilai x.

Pembahasan:
Agar a sejajar dengan b, perbandingan komponennya harus sama:
a₁ / b₁ = a₂ / b₂
x / 3 = 6 / -9

Sekarang kita selesaikan persamaan untuk mencari x:
x / 3 = 6 / -9
x / 3 = -2 / 3 (Sederhanakan 6/-9)
x = 3 * (-2 / 3)
x = -2

Jadi, agar vektor a sejajar dengan vektor b, nilai x haruslah -2. Vektor a akan menjadi <-2, 6>.

Kita bisa cek:
a = <-2, 6>
b = <3, -9>
-2 / 3
6 / -9 = -2 / 3
Perbandingannya sama, jadi sejajar.

Soal 3: Menentukan Vektor yang Searah/Berlawanan

Diberikan vektor m = <2, 5> dan vektor n = <4, 10>.
a. Tentukan apakah m dan n searah atau berlawanan arah.
b. Jika ada, tentukan vektor p yang berlawanan arah dengan m dan memiliki panjang dua kali panjang m.

Pembahasan:
a. Perbandingan komponen m dan n:
m₁ / n₁ = 2 / 4 = 1/2
m₂ / n₂ = 5 / 10 = 1/2

Karena perbandingannya sama (1/2) dan nilainya positif, maka vektor m dan n adalah searah.
Ini berarti n = 2m.

b. Kita ingin mencari vektor p yang berlawanan arah dengan m dan memiliki panjang dua kali panjang m.
Berlawanan arah berarti skalar perkaliannya harus negatif.
Panjang dua kali panjang m berarti magnitudo p adalah 2 * |m|.

Jika p berlawanan arah dengan m dan memiliki magnitudo dua kali lipat, maka p = -2m.
p = -2 * <2, 5>
p = <-4, -10>

Jadi, vektor p yang memenuhi adalah <-4, -10>.

Soal 4: Perbandingan Vektor dalam Konteks Geometri (Segitiga/Jajar Genjang)

Dalam segitiga ABC, D adalah titik tengah sisi AB dan E adalah titik tengah sisi AC. Tunjukkan bahwa vektor DE sejajar dengan vektor BC dan panjang DE adalah setengah panjang BC.

Pembahasan:
Kita dapat menggunakan vektor posisi. Misalkan titik A adalah titik pangkal (vektor posisi $veca$).
Maka, vektor posisi B adalah $vecb$ dan vektor posisi C adalah $vecc$.

Karena D adalah titik tengah AB, maka vektor posisi D adalah $vecd = fracveca + vecb2$.
Karena E adalah titik tengah AC, maka vektor posisi E adalah $vece = fracveca + vecc2$.

Sekarang kita cari vektor DE:
$vecDE = vece – vecd$
$vecDE = fracveca + vecc2 – fracveca + vecb2$
$vecDE = frac(veca + vecc) – (veca + vecb)2$
$vecDE = fracveca + vecc – veca – vecb2$
$vecDE = fracvecc – vecb2$

Sekarang kita cari vektor BC:
$vecBC = vecc – vecb$

Dari hasil di atas, kita lihat bahwa $vecDE = frac12(vecc – vecb)$.
Ini berarti $vecDE = frac12vecBC$.

Karena $vecDE$ dapat dinyatakan sebagai kelipatan skalar dari $vecBC$ (dengan skalar 1/2), maka:

1. Vektor DE sejajar dengan vektor BC.
2. Panjang DE adalah $frac12$ kali panjang BC (karena skalar 1/2 adalah positif, arahnya sama).

Ini adalah hasil dari teorema garis pertengahan pada segitiga.

Soal 5: Vektor di Ruang Tiga Dimensi

Diketahui vektor r = <2, -4, 6> dan vektor s = <-3, 6, -9>. Tentukan apakah vektor r dan s sejajar.

Pembahasan:
Kita akan menggunakan metode perbandingan komponen.
r₁ / s₁ = 2 / -3 = -2/3
r₂ / s₂ = -4 / 6 = -2/3
r₃ / s₃ = 6 / -9 = -2/3

Karena perbandingan semua komponen menghasilkan nilai yang sama (-2/3), maka vektor r dan s sejajar.
Ini berarti r = -2/3 s, atau s = -3/2 r. Vektor ini berlawanan arah karena skalar perkaliannya negatif.

5. Aplikasi Perbandingan Vektor dalam Kehidupan Nyata

Konsep perbandingan vektor bukan sekadar teori matematika, tetapi memiliki banyak aplikasi praktis:

• Fisika: Dalam mekanika, gaya, kecepatan, dan percepatan adalah besaran vektor. Mengetahui apakah dua gaya sejajar dapat menentukan apakah gaya-gaya tersebut bekerja searah atau berlawanan, yang sangat penting dalam menghitung gaya resultan. Dua mobil yang bergerak pada lintasan yang sama tetapi berlawanan arah dapat digambarkan dengan vektor kecepatan yang berlawanan.

• Grafika Komputer: Dalam pembuatan animasi dan permainan video, perbandingan vektor digunakan untuk menentukan arah pergerakan objek, orientasi kamera, dan bagaimana objek berinteraksi satu sama lain. Misalnya, menentukan apakah dua objek akan bertabrakan dapat melibatkan perbandingan vektor posisi dan kecepatan mereka.

• Navigasi: Kapal atau pesawat terbang bergerak dengan arah dan kecepatan tertentu. Vektor digunakan untuk memodelkan pergerakan ini. Memahami perbandingan vektor arah dan kecepatan dapat membantu dalam menentukan posisi relatif dan memprediksi lintasan.

6. Kesimpulan

Memahami perbandingan koordinat dua vektor adalah langkah penting dalam menguasai aljabar vektor. Konsep kesederhanaan hubungan antara dua vektor melalui perkalian skalar membuka pintu untuk analisis geometris yang lebih mendalam. Dengan menguasai metode perbandingan komponen atau menggunakan skalar perkalian, siswa dapat dengan mudah menentukan apakah dua vektor sejajar, searah, atau berlawanan arah. Contoh-contoh soal yang telah dibahas memberikan gambaran konkret tentang penerapan konsep ini, mulai dari soal dasar hingga yang lebih kompleks, serta menunjukkan relevansinya dalam berbagai bidang ilmu dan teknologi.

Dengan latihan yang cukup dan pemahaman yang kuat terhadap konsep dasar, siswa kelas X akan mampu memecahkan berbagai permasalahan yang melibatkan perbandingan koordinat vektor dengan percaya diri.