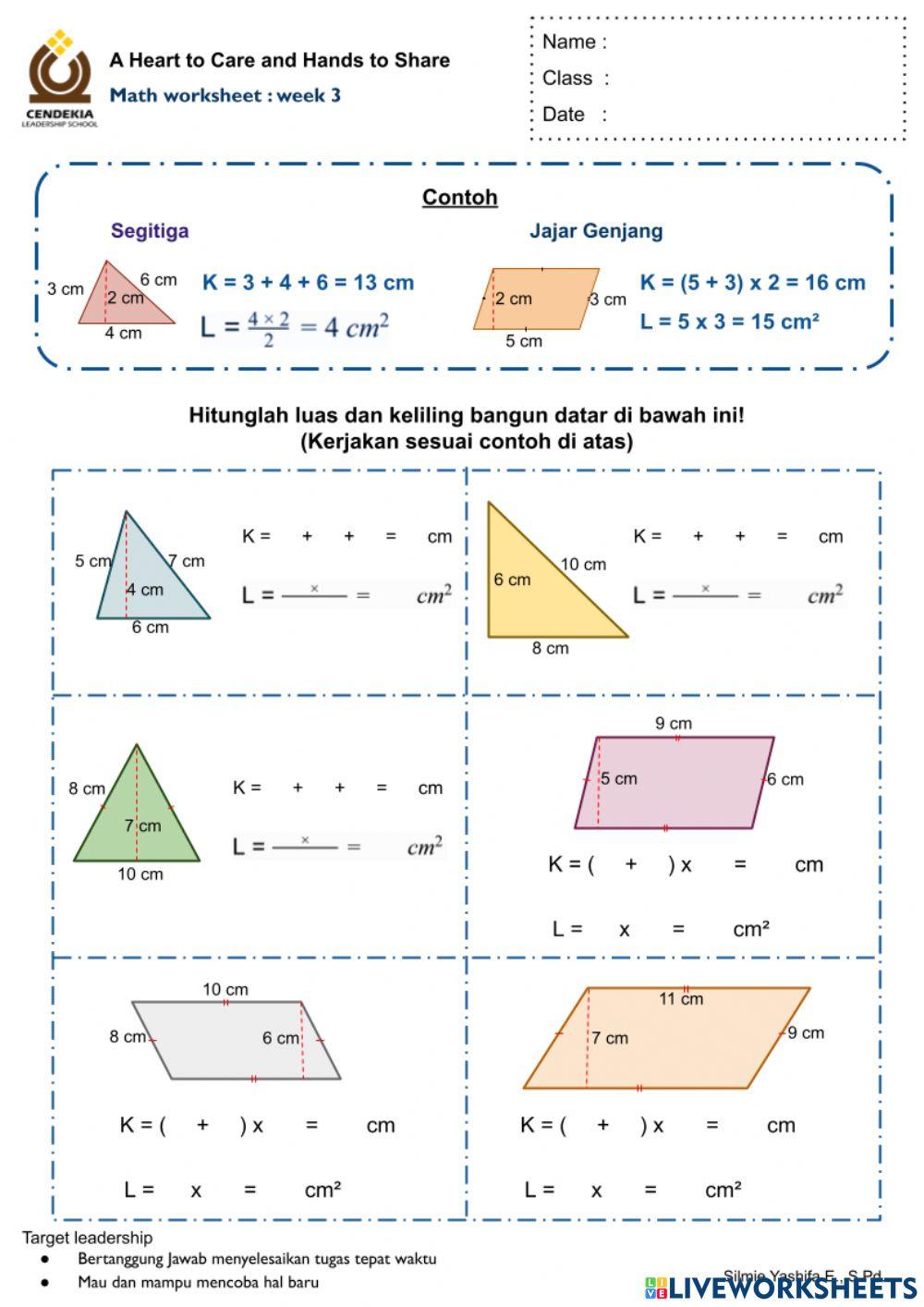
Menguasai Luas & Keliling Bangun Datar

Pendahuluan

Dalam dunia matematika, bangun datar merupakan salah satu konsep fundamental yang sangat penting untuk dipahami oleh siswa, terutama di jenjang Sekolah Dasar. Memahami luas dan keliling bangun datar bukan hanya sekadar menghafal rumus, melainkan melatih kemampuan berpikir logis, spasial, dan pemecahan masalah. Bagi siswa kelas 4 Sekolah Dasar, materi ini menjadi pijakan penting untuk mempelajari konsep geometri yang lebih kompleks di jenjang berikutnya. Artikel ini akan membahas secara mendalam mengenai latihan soal luas dan keliling bangun datar, dengan tujuan memberikan panduan yang jelas dan komprehensif bagi siswa, guru, maupun orang tua. Kita akan menjelajahi berbagai jenis bangun datar yang umum dipelajari di kelas 4, merinci rumus-rumus yang digunakan, serta menyajikan berbagai variasi soal latihan yang disertai dengan pembahasan.

I. Memahami Konsep Luas dan Keliling Bangun Datar

Sebelum kita melangkah lebih jauh ke latihan soal, sangat penting untuk memastikan pemahaman dasar mengenai apa itu luas dan keliling.

• Keliling: Keliling sebuah bangun datar adalah total panjang garis tepi yang membentuk bangun tersebut. Bayangkan seperti mengukur panjang pagar yang mengelilingi sebuah taman. Keliling selalu diukur dalam satuan panjang, seperti sentimeter (cm), meter (m), atau kilometer (km).

• Luas: Luas sebuah bangun datar adalah ukuran seberapa banyak ruang dua dimensi yang ditempati oleh bangun tersebut. Bayangkan seperti mengukur seberapa banyak ubin yang dibutuhkan untuk menutupi lantai sebuah ruangan. Luas selalu diukur dalam satuan luas, seperti sentimeter persegi (cm²), meter persegi (m²), atau hektar (ha).

II. Bangun Datar yang Umum Dipelajari di Kelas 4

Di kelas 4, siswa biasanya diperkenalkan pada beberapa jenis bangun datar utama. Pemahaman terhadap ciri-ciri masing-masing bangun datar akan sangat membantu dalam menentukan rumus yang tepat untuk menghitung luas dan kelilingnya.

1. Persegi:

   • Ciri-ciri: Memiliki empat sisi yang sama panjang dan empat sudut siku-siku (90 derajat).
   • Rumus Keliling: Karena keempat sisinya sama panjang, keliling persegi dapat dihitung dengan menjumlahkan panjang keempat sisinya, atau dengan rumus:
     • Keliling = sisi + sisi + sisi + sisi
     • Keliling = 4 × sisi
   • Rumus Luas: Luas persegi adalah hasil perkalian panjang sisinya dengan dirinya sendiri:
     • Luas = sisi × sisi

2. Persegi Panjang:

   • Ciri-ciri: Memiliki empat sisi, di mana sisi-sisi yang berhadapan memiliki panjang yang sama dan sejajar. Memiliki empat sudut siku-siku.
   • Rumus Keliling: Keliling persegi panjang adalah jumlah panjang keempat sisinya. Karena ada sepasang sisi panjang dan sepasang sisi lebar, rumusnya adalah:
     • Keliling = panjang + lebar + panjang + lebar
     • Keliling = 2 × (panjang + lebar)
   • Rumus Luas: Luas persegi panjang dihitung dengan mengalikan panjangnya dengan lebarnya:
     • Luas = panjang × lebar

3. Segitiga:

   • Ciri-ciri: Memiliki tiga sisi dan tiga sudut. Jenis-jenis segitiga beragam (segitiga sama sisi, sama kaki, siku-siku, sembarang), namun rumus dasar luas dan kelilingnya relatif umum.
   • Rumus Keliling: Keliling segitiga adalah jumlah panjang ketiga sisinya:
     • Keliling = sisi a + sisi b + sisi c
   • Rumus Luas: Luas segitiga dihitung dengan setengah dari hasil perkalian alas dengan tingginya:
     • Luas = ½ × alas × tinggi

4. Lingkaran (Pengenalan Dasar):

   • Ciri-ciri: Merupakan bangun datar yang terbentuk dari semua titik yang berjarak sama dari satu titik pusat.
   • Rumus Keliling (Konsep Awal): Di kelas 4, siswa mungkin diperkenalkan pada konsep keliling lingkaran, yang sering disebut sebagai "panjang busur" atau "keliling lingkaran". Rumus yang lebih formal menggunakan konstanta pi (π ≈ 22/7 atau 3.14) dan jari-jari (r) atau diameter (d):
     • Keliling = 2 × π × r
     • Keliling = π × d
   • Rumus Luas (Konsep Awal): Konsep luas lingkaran juga diperkenalkan, dengan rumus:
     • Luas = π × r²
   • Catatan: Untuk kelas 4, soal lingkaran biasanya masih dalam bentuk pengenalan konsep atau menggunakan pendekatan yang lebih sederhana jika tidak melibatkan nilai pi secara mendalam.

III. Latihan Soal Luas dan Keliling Bangun Datar

Bagian ini akan menyajikan berbagai contoh soal latihan yang bervariasi, mulai dari yang paling sederhana hingga yang sedikit menantang, beserta pembahasannya. Ini akan membantu siswa mempraktikkan pemahaman mereka tentang rumus dan penerapannya.

A. Latihan Soal Persegi

1. Soal 1: Sebuah taman berbentuk persegi memiliki panjang sisi 10 meter. Berapakah keliling dan luas taman tersebut?

   • Pembahasan:
     • Diketahui: sisi = 10 meter
     • Keliling = 4 × sisi = 4 × 10 meter = 40 meter
     • Luas = sisi × sisi = 10 meter × 10 meter = 100 meter persegi
     • Jadi, keliling taman adalah 40 meter dan luasnya adalah 100 meter persegi.

2. Soal 2: Ibu membeli taplak meja berbentuk persegi dengan luas 81 cm². Berapakah panjang sisi taplak meja tersebut? Berapa kelilingnya?

   • Pembahasan:
     • Diketahui: Luas = 81 cm²
     • Untuk mencari sisi, kita perlu mencari bilangan yang jika dikalikan dengan dirinya sendiri menghasilkan 81. Bilangan tersebut adalah 9 (karena 9 × 9 = 81). Jadi, sisi = 9 cm.
     • Keliling = 4 × sisi = 4 × 9 cm = 36 cm
     • Jadi, panjang sisi taplak meja adalah 9 cm dan kelilingnya adalah 36 cm.

B. Latihan Soal Persegi Panjang

1. Soal 3: Sebuah lapangan sepak bola memiliki panjang 100 meter dan lebar 50 meter. Hitunglah keliling dan luas lapangan tersebut.

   • Pembahasan:
     • Diketahui: panjang = 100 meter, lebar = 50 meter
     • Keliling = 2 × (panjang + lebar) = 2 × (100 meter + 50 meter) = 2 × 150 meter = 300 meter
     • Luas = panjang × lebar = 100 meter × 50 meter = 5.000 meter persegi
     • Jadi, keliling lapangan adalah 300 meter dan luasnya adalah 5.000 meter persegi.

2. Soal 4: Sebuah buku memiliki keliling 40 cm. Jika panjang buku tersebut adalah 12 cm, berapakah lebarnya? Berapa luas buku tersebut?

   • Pembahasan:
     • Diketahui: Keliling = 40 cm, panjang = 12 cm
     • Kita gunakan rumus keliling: Keliling = 2 × (panjang + lebar)
     • 40 cm = 2 × (12 cm + lebar)
     • Bagi kedua sisi dengan 2: 20 cm = 12 cm + lebar
     • Untuk mencari lebar, kurangi 20 cm dengan 12 cm: lebar = 20 cm – 12 cm = 8 cm.
     • Luas = panjang × lebar = 12 cm × 8 cm = 96 cm persegi
     • Jadi, lebar buku tersebut adalah 8 cm dan luasnya adalah 96 cm persegi.

C. Latihan Soal Segitiga

1. Soal 5: Sebuah segitiga memiliki panjang sisi 7 cm, 8 cm, dan 9 cm. Berapakah keliling segitiga tersebut?

   • Pembahasan:
     • Diketahui: sisi a = 7 cm, sisi b = 8 cm, sisi c = 9 cm
     • Keliling = sisi a + sisi b + sisi c = 7 cm + 8 cm + 9 cm = 24 cm
     • Jadi, keliling segitiga tersebut adalah 24 cm.

2. Soal 6: Sebuah segitiga memiliki alas sepanjang 15 cm dan tingginya 10 cm. Berapakah luas segitiga tersebut?

   • Pembahasan:
     • Diketahui: alas = 15 cm, tinggi = 10 cm
     • Luas = ½ × alas × tinggi = ½ × 15 cm × 10 cm = ½ × 150 cm persegi = 75 cm persegi
     • Jadi, luas segitiga tersebut adalah 75 cm persegi.

D. Latihan Soal Gabungan dan Aplikasi

Soal-soal ini menggabungkan beberapa bangun datar atau menerapkan konsep luas dan keliling dalam skenario dunia nyata.

1. Soal 7: Sebuah kolam renang berbentuk persegi panjang berukuran 20 meter × 10 meter. Di sekeliling kolam renang akan dipasangi keramik dengan lebar 1 meter. Berapakah luas keramik yang dibutuhkan?

   • Pembahasan:
     • Ini adalah soal yang sedikit lebih menantang. Kita perlu mencari luas area yang lebih besar (kolam + keramik) lalu menguranginya dengan luas kolam renang.
     • Ukuran kolam renang: panjang = 20 m, lebar = 10 m.
     • Karena keramik dipasang di sekeliling kolam dengan lebar 1 meter, maka ukuran kolam yang diperluas dengan keramik menjadi:
       • Panjang baru = 20 m + 1 m (kiri) + 1 m (kanan) = 22 meter
       • Lebar baru = 10 m + 1 m (atas) + 1 m (bawah) = 12 meter
     • Luas kolam renang = 20 m × 10 m = 200 m²
     • Luas area kolam renang beserta keramik = 22 m × 12 m = 264 m²
     • Luas keramik yang dibutuhkan = Luas area baru – Luas kolam = 264 m² – 200 m² = 64 m²
     • Jadi, luas keramik yang dibutuhkan adalah 64 meter persegi.

2. Soal 8: Sebuah kebun berbentuk persegi dengan panjang sisi 15 meter. Sebagian kebun tersebut ditanami sayuran seluas 50 meter persegi. Berapakah sisa luas kebun yang tidak ditanami sayuran?

   • Pembahasan:
     • Diketahui: Luas total kebun (persegi) = 15 m × 15 m = 225 m²
     • Luas ditanami sayuran = 50 m²
     • Sisa luas kebun = Luas total kebun – Luas ditanami sayuran
     • Sisa luas kebun = 225 m² – 50 m² = 175 m²
     • Jadi, sisa luas kebun yang tidak ditanami sayuran adalah 175 meter persegi.

3. Soal 9: Sebuah pita sepanjang 60 cm akan digunakan untuk menghias tepi sebuah taplak meja berbentuk persegi panjang dengan panjang 15 cm. Berapakah panjang taplak meja yang dapat dihias jika lebarnya adalah 10 cm? (Soal ini bisa diinterpretasikan sebagai mencari sisa pita atau panjang yang terpakai). Mari kita asumsikan soal ini menanyakan panjang tepi yang bisa dihias dari pita yang ada.

   • Pembahasan:
     • Ini adalah soal terbalik yang menguji pemahaman. Pita 60 cm adalah total panjang yang tersedia.
     • Keliling taplak meja = 2 × (15 cm + 10 cm) = 2 × 25 cm = 50 cm.
     • Jika kita hanya mempertimbangkan panjang sisi yang akan dihias, dan pita yang tersedia adalah 60 cm, maka pita tersebut cukup untuk menghias keliling taplak meja.
     • Namun, jika soalnya adalah: "Sebuah taplak meja berbentuk persegi panjang memiliki panjang 15 cm dan lebar 10 cm. Jika pita sepanjang 60 cm digunakan untuk menghias tepinya, berapa sisa panjang pita?"
       • Keliling taplak meja = 50 cm.
       • Sisa pita = 60 cm – 50 cm = 10 cm.

IV. Tips dan Trik dalam Mengerjakan Soal Luas dan Keliling

• Pahami Soal dengan Baik: Baca soal berulang kali. Identifikasi bangun datar apa yang dibicarakan, apa yang diketahui (panjang, lebar, sisi, alas, tinggi), dan apa yang ditanyakan (luas atau keliling).
• Gambarkan Bangun Datar: Jika soal terasa abstrak, cobalah menggambar bangun datarnya. Ini sangat membantu untuk memvisualisasikan masalah. Untuk soal gabungan, gambarkan semua bagiannya.
• Tuliskan Rumus yang Tepat: Setelah mengidentifikasi bangun datar dan apa yang ditanyakan, tuliskan rumus yang sesuai.
• Perhatikan Satuan: Pastikan satuan yang digunakan konsisten. Jika panjang dalam meter, maka luas akan dalam meter persegi. Jangan sampai tertukar antara satuan panjang dan satuan luas.
• Latihan Rutin: Semakin sering berlatih, semakin terbiasa siswa dengan berbagai jenis soal dan semakin cepat mereka dalam menerapkan rumus.
• Gunakan Alat Bantu (Jika Diperbolehkan): Penggaris bisa membantu dalam menggambar, dan kalkulator (jika diizinkan) bisa membantu dalam perhitungan. Namun, penting untuk tetap memahami proses perhitungannya.
• Variasikan Tingkat Kesulitan: Mulailah dari soal yang mudah, lalu secara bertahap tingkatkan kesulitannya. Ini membangun kepercayaan diri siswa.

V. Kesimpulan

Menguasai konsep luas dan keliling bangun datar merupakan keterampilan penting yang akan terus digunakan siswa dalam berbagai aspek matematika dan kehidupan sehari-hari. Melalui latihan soal yang terstruktur dan bervariasi, siswa kelas 4 dapat membangun pemahaman yang kuat, meningkatkan kemampuan pemecahan masalah, dan menumbuhkan rasa percaya diri dalam menghadapi tantangan matematika. Dengan panduan yang tepat dari guru dan dukungan dari orang tua, materi ini dapat menjadi pengalaman belajar yang menyenangkan dan bermakna. Ingatlah, kunci utamanya adalah pemahaman konsep, penerapan rumus yang tepat, dan latihan yang konsisten.